为积极响应教育数字化战略行动，推动信息技术与数学学科的深度融合，助力教师掌握动态数学工具在探究式教学中的创新应用，提升教师对集几何绘图、代数计算、数据可视化于一体的专业数学软件的操作能力，应用数学教研室特邀数学团队教师张小娟，于 4 月 16 日在行者楼 104 室为团队教师开展 “GeoGebra 数学软件示范培训会”。此次培训聚焦高等数学课程中“空间解析几何”章节，系统展示了 GeoGebra 在教学场景中的多样化实操技巧。

一、空间直角坐标系：从“抽象框架”到“交互工具”的认知升级

在传统教学中学生对空间直角坐标系的卦限分布、点坐标位置、几何意义等的理解往往停留在机械记忆层面，为打破此壁垒，建立空间框架，张老师通过 Geogebra 的“3D 绘图区属性”功能演示如何将静态坐标系转化为可操作、可感知的教学工具：

在属性栏中勾选“显示坐标轴”，分别拖动 x 轴、y 轴、z 轴的箭头端点，实时改变轴长比例（如将 x 轴长度设为 2，y 轴设为 1.5，z 轴设为 3），直观展示“不等比例坐标轴”对图形视觉呈现的影响；双击坐标轴标签，修改轴名（如将 z 轴改为 “高度轴”），并设置标签颜色（如红色 x 轴、蓝色 y 轴、绿色 z 轴），利用色彩差异增强学生对三轴的辨识度。

还可通过“几何输入”指令生成八个卦限的透明立方体（如输入 “半空间 x>0”“半空间 y>0”“半空间 z>0”的交集），分别填充不同透明度的色块；点击任一卦限区域，Geogebra 自动显示该卦限的坐标符号特征（如第一卦限 x>0,y>0,z>0），配合“闪烁”动画效果，帮助学生记忆各卦限的位置关系。此外，在指令栏输入点的坐标（如“点 A=(3,-2,4)”），Geogebra 自动在 3D 绘图区标出点 A，并显示其到各坐标平面的距离（如到 x-y 平面距离为 4，到 y-z 平面距离为 3），可以帮助学生强化对空间方位的理解和认知。

二、动态建模：从方程到图形的“可视化翻译”

在代数区输入平面一般式方程 Ax + By + Cz + D = 0，通过滑动条动态调整系数 A、B、C、D 的值，几何区同步呈现平面的位置与朝向变化。当演示“D=0时平面过原点”、“当A=0 时平面平行于 x 轴”等特殊情形时，大家可直观观察到系数取值对平面位置的决定性作用，破解了传统教学中“学生难想象、教师难比划”的痛点。

以“圆柱面 x2 + y2 = R2”为例，老师可先通过“轨迹”工具绘制xoy坐标平面上的圆，再利用“沿向量拉伸”功能生成三维柱面；针对旋转曲面，以“直线绕坐标轴旋转生成圆锥面”为例，通过“旋转体”指令快速生成图形，并对比不同母线与旋转轴夹角对曲面形状的影响，让抽象的“运动生成曲面”概念变得可操作、可观察。

三、截痕法：用动态剖切解析二次曲面本质

“截痕法研究二次曲面”内容，张老师以椭球面 x2/a2+ y2/b2 + z2/c2 = 1 为例，演示如何通过 Geogebra 的 “截面” 工具动态展示不同平面截切曲面的轨迹：在 3D 绘图区输入椭球面方程，默认显示完整曲面；添加“平面 z=k”滑动条（k∈[-c,c]），实时展示水平截痕从点（k=±c）到椭圆（|k|<c）的变化过程；同理添加 “平面 x=m”“平面 y=n” 滑动条，对比不同方向截痕的形状差异；利用“轨迹动画”功能，让截平面沿坐标轴匀速移动，自动生成截痕变化的动态视频，通过 Geogebra 可在分钟级完成动态建模，且能随时暂停、旋转视角，可极大提升教学效率和教学效果。

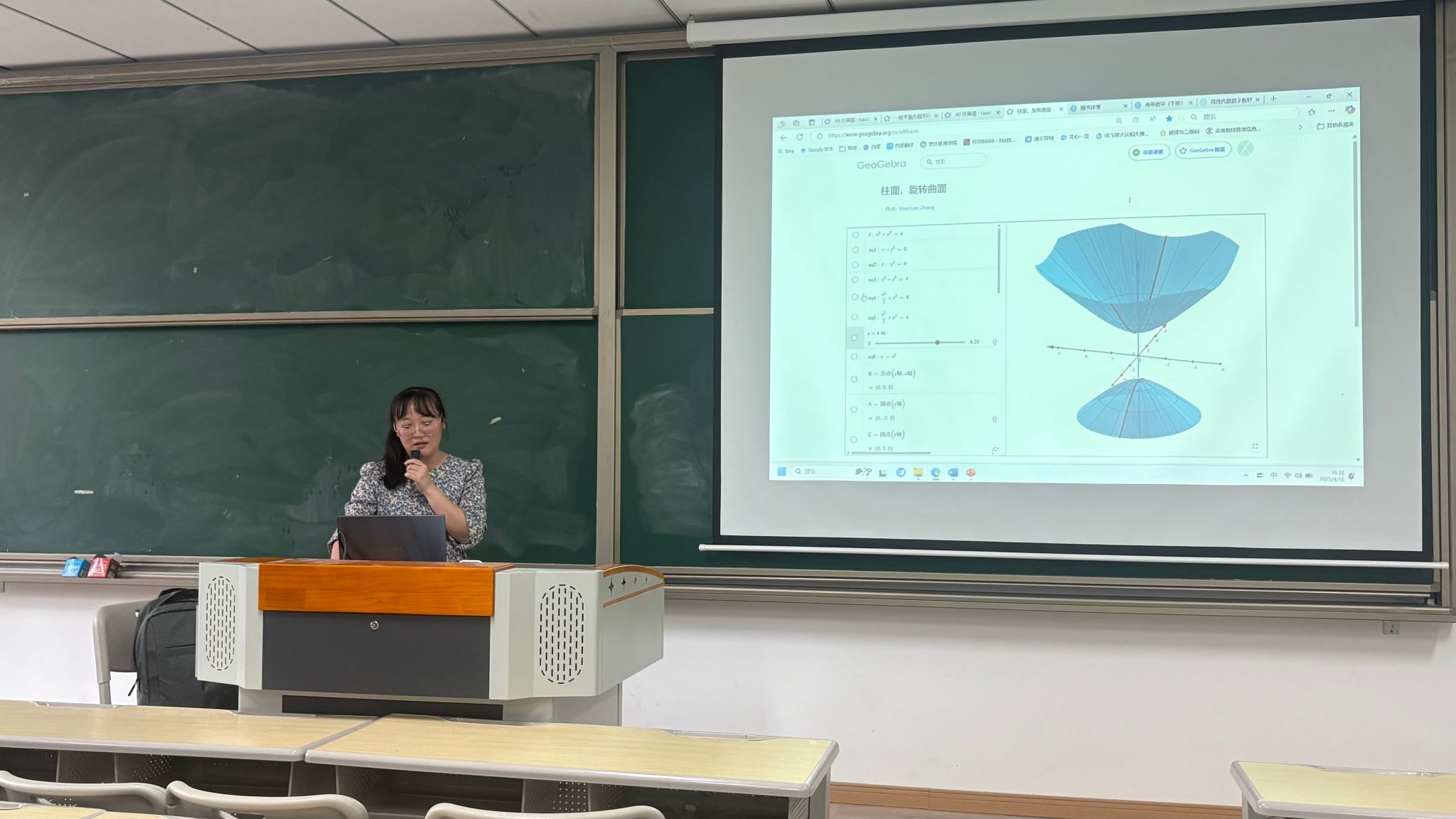
Geogebra 不仅是绘图工具，更是连接代数思维与几何直观的数字桥梁，通过动态建模，教师可引导学生从记忆方程形式转向理解几何本质，这也与“以学生为中心”的教学理念高度契合。我们学到的不仅是软件的操作，更是让数学变得可触摸、动起来的技能，希望团队教师不断加强技能训练，在教学中进行实践，让课堂有趣且生动。

图片：童画

撰稿：杨森

审稿：边梦柯

排版：刘亚涛

数理教学部供稿